inclination measurement |
|
Table of contents We have seen from the Table 3 that the calculation of the azimuth is hardly dependent to the tilt value. The purpose of this part is to implement a system to measure the inclination of the robot to counter-act this effect. The accelerometer is the simplest way to obtain the tilt value. 7.1. The accelerometer’s operation modeWhen the accelerometer is stationary (no lateral or vertical acceleration are present) the only force acting on the sensor is the earth gravity. The inclination is then the angle between the gravitational force and the sensitive axis. Since this axis lies on a horizontal plane, the inclination can be measured from any initial accelerometer orientation. Therefore, we have the choice to design our accelerometer initial position either on a vertical or horizontal PCB:
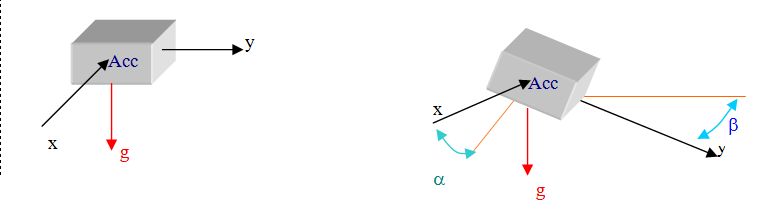
Figure 16: Two-axis inclination from horizontal
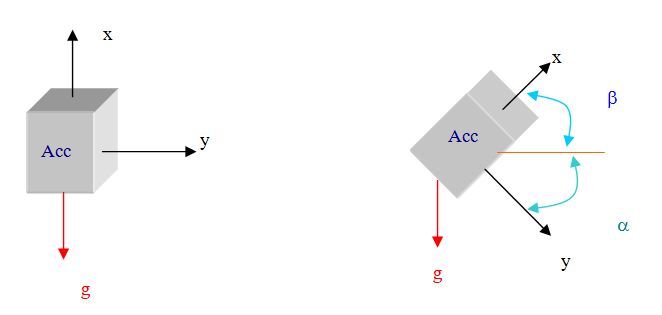
Figure 17: One axis inclination from vertical While the first configuration (Figure 16) is limited to an angle of 60° on to two axis, the second configuration (Figure 17) get a better resolution through 360° arc but on only one axis. Consequently, this last solution requires two accelerometers to detect the tilt according two axis. This solution increases the cost and the space on the PCB. In our application, the inclination angle should never exceed ± 30° from the horizontal. Regarding this consideration, the first configuration has been chosen to design the inclination measurement system. The Equation 6 gives the measure of the inclination:
a: Inclination angle [radian] A: Accelerometer outputs [N.m-1] G: The earth gravity [N.m-1] Equation 6 After calculation, the accelerometer will then be able to measure the inclination with a precision below 0,1°. However, an acceleration of the robot will introduce a noise. A post treatment needs to be applied: - A low pass filter is a first hint. Indeed, acceleration leads to an important variation during a short time contrary to the tilt that must be a progressive variation during a long time. - Indirectly, the gyro will also make the difference. - The value of the acceleration could also be directly sent from the odometry. - To use of a third axis that will vary only if the acceleration detected on the horizontal plan is due to an inclination. 7.2. The selection of the accelerometerTo detect the tilt we have chosen to use a 2-axis accelerometer. Consequently, the one-axis sensors have been eliminated of our selection. We first looked the characteristics of the accelerometer proposed by Analog Devices (already implemented on the UAV):
Table 4: Accelerometers from Analog Devices To compare the competitiveness of these last ones, we have looked for different other components available on the market:
Table 5: Accelerometers from Memsic and Kionix The accelerometers from Kionix and Analog Devices have similar results in test (low noise and high sensitivity) and better characteristics than the products of Memsic. Nevertheless, these last ones offer additional an output such as a temperature and a voltage reference (only for the MXA2500ML). In consequence, for a conception facility we have decided to implement this accelerometer.
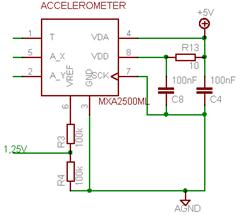
7.3. Design of the systemAt 0g, the signal in the output of the signal equals to 1,25V and it vary around this value, whereas the signal in the input of the ADC should be centred in 2,048V. In addition, low pass filter has to be applied on these signals. An amplification and a filter will be used as shown on the Figure 7: Amplification schematic 1 with a INA2126 amplifier.
Figure 18: The tilt's circuit 7.3.1. The filterThe datasheet of the MXA2500ML recommend filtering each signal at 200 Hz to eliminate the noise floors: f = 1 / (2pRC) and R = 40kW Þ C = 1,98.108 Note: The value of R corresponds to the value of the INA2126’s inner resistor. The normalised value 22nF for the capacitor has been chosen and therefore we have obtained a low pass filter at 180Hz. 7.3.2. The amplificationThe gain G of the previous circuit is adjusted by the value of the resistance Rgain according to the following equation: G = R / Rgain. This gain should not be superior to a maximum gain to avoid that the variation of the acceleration below 2,048V. The typical sensitivity of this device is 500mV/g at 25°C. However, this characteristic changes over temperature according the following equation: Si * Ti = Sf * Tf
Si and Sf are the initial and current sensitivity Ti and Tf initial and current temperature Equation 7 Consequently, we consider the maximum variation of temperature possible 50°. Then the maximum value for the sensitivity could be: Sf = (Si * TI) / Tf Þ Sf » 600mV/g As the measurement range is ±1g, we can deduce that the maximum variation will be ±600mV. Then the maximum gain authorised is: Gmax = 2048 / 600 Þ Gmax < 3,4 Then Rgainmin = R / Gmax Þ Rgainmin » 11,05kW Therefore we have chosen the normalised value 13kW for the resistance Rgain and we have then a gain equals to 3,08. We can consider that the maximum noise density will be equal to 0,4mg/ÖHz on the bandwidth of the frequency response (20Hz). So we can calculate the rms noise from this information: Noise [mg rms] = Noise density [mg/ÖHz] * Ö(Bandwidth [Hz] * 1,6) Þ Noisemax » 2,26 mg rms Þ Noise » 1,13 mV The maximum value of the noise amplified in the response frequency is about 3,4mV. 7.3.3. The voltage and the temperature referenceOne of the reasons why we chose this component is that it offers a voltage and a temperature reference. The value of this last one is send to the microcontroller (on the card 1 and on the MAX186 on the card 2) and will allow us to compensate the derive of the acceleration’s output due to the variation of the temperature and to calibrate correctly this device from this value. The voltage reference is used to calculate the acceleration on each axis. The 0g output is equals to 1,25V, which corresponds to this reference divided by two. It follows that we will refer to this voltage to amplify the output variation. |